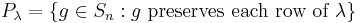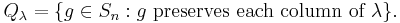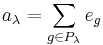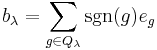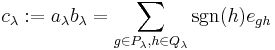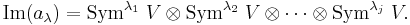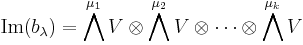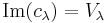Young symmetrizer

In mathematics, a Young symmetrizer is an element of the group algebra of the symmetric group, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex numbers. A similar construction works over any field, and the resulting representations are called Specht modules. The Young symmetrizer is named after British mathematician Alfred Young.

Contents

Definition

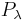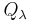Given a finite symmetric group Sn and specific Young tableau λ corresponding to a numbered partition of n, define two permutation subgroups P_\lambda and Q_\lambda of Sn as follows:

P_\lambda=\{ g\in S_n�: g \text{ preserves each row of } \lambda \}

and

Q_\lambda=\{ g\in S_n�: g \text{ preserves each column of } \lambda \}.

Corresponding to these two subgroups, define two vectors in the group algebra 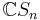\mathbb{C}S_n as

a_\lambda=\sum_{g\in P_\lambda} e_g

and

b_\lambda=\sum_{g\in Q_\lambda} \sgn(g) e_g

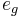where e_g is the unit vector corresponding to g, and 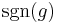\sgn(g) is the signature of the permutation. The product

c_\lambda�:= a_\lambda b_\lambda = \sum_{g\in P_\lambda,h\in Q_\lambda} \sgn(h) e_{gh}

is the Young symmetrizer corresponding to the Young tableau λ. Each Young symmetrizer corresponds to an irreducible representation of the symmetric group, and every irreducible representation can be obtained from a corresponding Young symmetrizer. (If we replace the complex numbers by more general fields the corresponding representations will not be irreducible in general.)

Construction

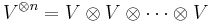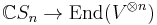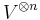Let V be any vector space over the complex numbers. Consider then the tensor product vector space V^{\otimes n}=V \otimes V \otimes \cdots \otimes V (n times). Let Sn act on this tensor product space by permuting each index. One then has a natural group algebra representation \mathbb{C}S_n \rightarrow \text{End} (V^{\otimes n}) on endomorphisms on V^{\otimes n}.

Given a partition λ of n, so that 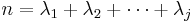n=\lambda_1%2B\lambda_2%2B \cdots %2B\lambda_j, then the image of 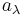a_\lambda is

\text{Im}(a_\lambda) = \text{Sym}^{\lambda_1}\; V \otimes \text{Sym}^{\lambda_2}\; V \otimes \cdots \otimes \text{Sym}^{\lambda_j}\; V.

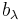The image of b_\lambda is

\text{Im}(b_\lambda) = \bigwedge^{\mu_1} V \otimes \bigwedge^{\mu_2} V \otimes \cdots \otimes \bigwedge^{\mu_k} V

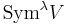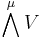where μ is the conjugate partition to λ. Here, \text{Sym}^{\lambda} V and \bigwedge^{\mu} V are the symmetric and alternating tensor product spaces.

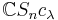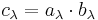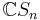The image \mathbb{C}S_nc_\lambda of c_\lambda = a_\lambda \cdot b_\lambda in \mathbb{C}S_n is an irreducible representation[1] of Sn, called a Specht module. We write

\text{Im}(c_\lambda) = V_\lambda

for the irreducible representation.

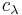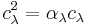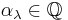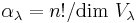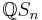Some scalar multiple of c_\lambda is idempotent, that is c^2_\lambda = \alpha_\lambda c_\lambda for some rational number \alpha_\lambda\in\mathbb{Q}. Specifically, one finds \alpha_\lambda=n! / \text{dim } V_\lambda. In particular, this implies that representations of the symmetric group can be defined over the rational numbers; that is, over the rational group algebra \mathbb{Q}S_n.

Consider, for example, S3 and the partition (2,1). Then one has 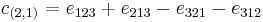c_{(2,1)} = e_{123}%2Be_{213}-e_{321}-e_{312}

If V is a complex vector space, then the images of 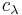c_\lambda on spaces Vd provides essentially all the finite-dimensional irreducible representations of GL(V).

See also

Notes

  1. ^ See (Fulton & Harris 1991, Theorem 4.3, p. 46)

References